逻辑回归&&贝叶斯优化

一、简介

（一）逻辑回归

1.浅浅分析

逻辑回归中，响应变量描述了结果是正向情况的概率。如果响应变量等于或者超过了一个区分阈值，则被预测为正向类。

而逻辑函数总是返回一个0-1之间的值。

个人理解：设置一个界限，等于或者超过这个界限的，被定义为比较好的，将比较好的概率以小数形式输出。

2.应用

我们在sklearn库中可以使用LogisticsRegression类来进行逻辑回归训练

参考文献：scikit-learn机器学习五（逻辑回归与朴素贝叶斯）

（二）朴素贝叶斯

1.朴素贝叶斯

（1）朴素贝叶斯的两个基本假设：

1. 独立：一个特征出现的可能性和与它和其他特征相邻没有关系

2. 每个特征同等重要

参考文献：机器学习—朴素贝叶斯及其优化

（2）公式

注:

W：特征值

C：类别

补充知识：

条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率，记作：P(A|B)

特性：P(A1,A2|B)= P(A1|B)P(A2|B)

注意：此条件概率的成立，是由于A1，A2相互独立的结果

（3）应用

sklearn朴素贝叶斯实现API

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

参考文献：机器学习算法基础 DAY 4 朴素贝叶斯算法&算法调优

2.贝叶斯优化

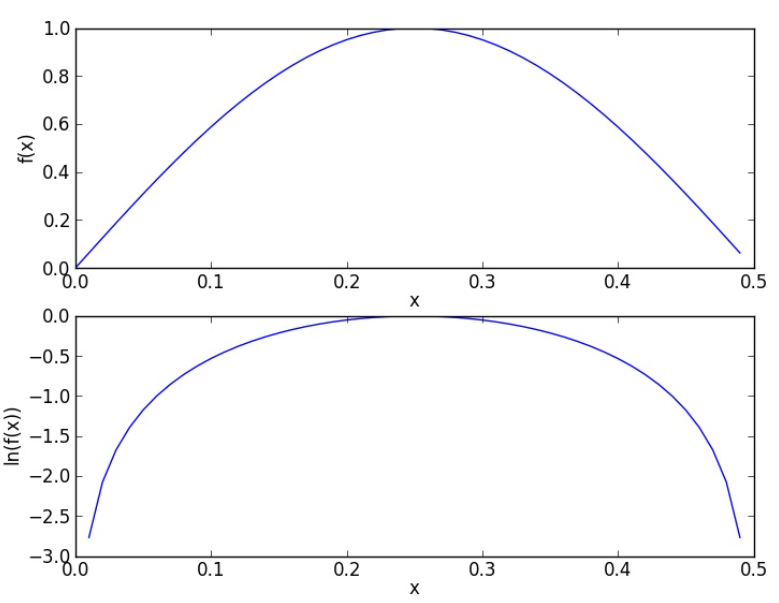
（1）将原有的概率变为对数

由于对数化了之后在[0.1]上值的变化更大了，这样就消除了概率计算下溢的风险。

log和原曲线增减性相同，且在同样的位置取到极值点，所以这样的替换是可行的。